在20世纪20年代，Kramers和Kronig发现，一个随频率变化的物理量$Z(\omega)$的实部$Z’(\omega)$和虚部$Z’’(\omega)$间存在一定关系，即Kramers–Kronig关系：

$Z(\omega) = Z'(\omega) + iZ''(\omega)$

$$ Z'(\omega) = \frac{1}{\pi} P \int^{\infty}_{-\infty} \frac{Z''(\omega')}{\omega'-\omega} \text{d}\omega' $$

$$ Z''(\omega) = -\frac{1}{\pi} P \int^{\infty}_{-\infty} \frac{Z'(\omega')}{\omega'-\omega} \text{d}\omega' $$

其中$P$表示柯西主值（Cauchy principle value）。

建议将本文与交流阻抗谱学与能源电化学一文一同食用~

Kramers–Kronig关系成立的四个条件

要得到以上关系，要求该物理系统满足以下四个条件：

因果性条件：物理体系只对所施加扰动进行响应。对信噪比有要求。
线性条件：物理体系的响应与施加扰动间为线性关系。施加扰动不可过大——在小扰动范围内，电压与电流近乎线性关系。
稳定性条件：对体系停止扰动后，体系能回到受扰动前的状态。施加扰动不可过大，从而使体系不转移到另一个状态。
有限性条件：随频率变化的物理量（阻抗）在全频率范围内（包括零和无穷大）都是有限值。部分RC电路不满足有限性条件，因此也不存在Kramers–Kronig关系。

Kramers–Kronig关系的证明

满足以上四个条件，复数的Kramers–Kronig关系便成为了纯数学问题。观察Kramers–Kronig关系，可以发现我们需要求解复变函数$f(x)$在$(\infty, -\infty)$范围内的积分：

$\int^{\infty}_{-\infty} \frac{f(x)}{x-\omega}\text{d}x$

解决该问题的一种相对简单的方式是构造积分域，并利用解析函数$f(x)$的积分与路径无关的特性。构造如下积分域：

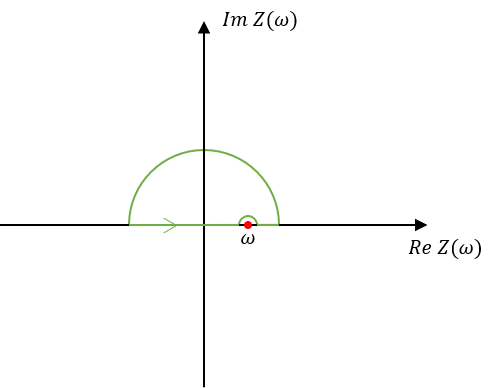
由Cauchy留数定理可得

$\oint \frac{Z(\omega')}{\omega'-\omega}\text{d}\omega'=0$

又由Sokhotski–Plemelj定理可得

$\oint \frac{Z(\omega')}{\omega'-\omega}\text{d}\omega' = P \int^{\infty}_{-\infty} \frac{Z(\omega')}{\omega'-\omega} \text{d}\omega' - i \pi Z(\omega) = 0$

关注笔者博客的同学可能记得，以上定理的离散函数形式在另一篇博文中也有应用：量子物理中的Green函数定义及其应用。

等式后半部分移项整理可得

$\begin{split} Z'(\omega) + iZ''(\omega) = Z(\omega) &= \frac{1}{i\pi} \int^{\infty}_{-\infty}\frac{Z(\omega')}{\omega'-\omega} \text{d}\omega' \\ &= \frac{1}{i\pi} \int^{\infty}_{-\infty}\frac{Z'(\omega') + iZ''(\omega')}{\omega'-\omega} \text{d}\omega' \\ &= \frac{1}{\pi} P \int^{\infty}_{-\infty} \frac{Z''(\omega')}{\omega'-\omega} \text{d}\omega' -i\frac{1}{\pi} P \int^{\infty}_{-\infty} \frac{Z'(\omega')}{\omega'-\omega} \text{d}\omega' \end{split}$

综上所述，等式两边复数的实部和虚部相对应便可得到Kramers–Kronig关系。

与电化学阻抗谱的关系

对线性电子元件系统来说，测试得到复阻抗的Kramers–Kronig关系一般都是能被满足的；但在电化学电极系统中，Kramers–Kronig关系成立的四个条件并不总是能够满足（如上讨论）。因此，可通过Kramers–Kronig关系来检验所获得电化学阻抗谱的可靠性。基于可靠的电化学阻抗谱数据，我们才能对系统的物理化学特性进行准确分析。

参考资料

[1] 曹楚南. 电化学阻抗谱导论[M]. 科学出版社, 2002.
[2] https://en.wikipedia.org/wiki/Kramers–Kronig_relations.