大家好啊。今天我们讨论一个电化学与数据的交叉主题哈。
大家在对材料进行电化学性能表征时,可能经常会使用到交流阻抗法。但大家是否曾好奇过“交流阻抗”是如何计算的呢?“阻抗”是一个直接观测量还是一个间接计算量?接下来,我们就要聊聊这个话题。
内容真挺难的,笔者没能完全hold住,很多内容其实都没有讨论得特别透彻。博主会继续更新相关技术内容。希望各领域的老师们不吝赐教!
从欧姆定律(Ohm’s Law)开始——纯电阻电路
德国物理学家Georg Ohm在 1827 年发表的一篇论文中描述了通过包含各种长度电线的简单电路测量施加的电压和电流。他提出,通过两点之间导体的电流与两点之间的电压成正比。
其中,$U$为电压,$I$为电流。$R$被认为是一种跟电子元件性质有关的比例常数,即电阻(Resistance)。在测试的绝大多数材料中,这一关系都能够成立。因此,欧姆定理作为一个经验公式可以得到广泛应用。但并不是所有的电子元件都能满足该性质。这给我们带来了疑问:除了电阻外,还有哪些电子元件?如何理解这些电子元器件的性质?
非纯电阻电路——交流阻抗的定义
电路的四大基本变量是电流$I$、电压$U$、电荷$Q$和磁通量$\Phi$。其中:
- 电阻(Resistor):表征电压与电流之间的关系;
- 电容(Capacitor):表征电量与电压之间的关系;
- 电感(Inductor):表征磁通量与电流之间的关系;
- 忆阻器(Memristor):表征磁通量与电荷之间的关系(最近大火的电子元件,笔者也很感兴趣,但不在本文讨论范围内)。
在直流电路中,电感短路,电容断路;欧姆定律没有描述电路中的电抗应该如何计算。很神奇的地方是,引入复阻抗后,对非纯电阻电路,交流电路中,阻抗的定义竟跟电阻很相似——引入电抗后,阻抗为电阻(实数)与电抗(虚数)之和,为一个复数:
从理论到工程——数字信号处理
在定义好交流电路中阻抗的具体定义后,接下来就是如何在实际生活中计算的问题了。我们知道,直接能够观测(或采集)的物理量是电压和电流。但根据阻抗的定义,$Z(\omega)$是一个复数,电压$U(t)$和电流$I(t)$也应该是复数。那么,电压和电流为何能够使用复数来进行表示呢?
这就涉及到接下来提及的一种数学工具了。通过这种数学工具,我们能够将采集到的离散(电压/电流)数据点转化为复数。
空间变换
笔者对“空间变换”的概念是在不断跨学科的过程中逐渐形成的:空间域到能量域(光的衍射),态矢量与能量(量子力学),特征值与特征向量(线性代数),时域到频域(信号处理)等等……貌似“空间变换”是一个很高大上的概念。
但实际上,我们很早就熟悉了空间变换的思想:比如,在解析几何中将笛卡尔(直角)坐标变换为极坐标,通过对数变换将乘法运算变换为加法运算等等。
Fourier变换(Fourier Transform)
Fourier级数(离散变量)
任何周期信号都可以通过多个三角波信号组合。
连续变量
从离散变量推广至连续变量,无限多个三角函数之和可以无限逼近任何周期信号。
欧拉公式(Euler’s Formula)
根据欧拉公式
任意三角函数都可以表示为一个复数。这也意味着,任何周期信号可以被一个复数所表示,也包括我们之前所提及的复阻抗$Z(\omega)$、交流电压$U(t)$和交流电流$I(t)$。
离散数据点的处理
真实信号中,由于信噪比不可能无穷大,而我们只对数字信号中的有效信号感兴趣,而不希望引入噪声。而一般地,信号频率与噪声频率存在差别(需要事先考虑设计),于是我们就能利用以下傅里叶变换方法,先把数字信号从时域转换到频域,就能够提取到指定频率信号。该信号以复数形式呈现。
由以上推导,通过下式得出时域到频域的变换公式:
其中,$F(\omega)$为频域函数,$f(t)$为时域函数。
通过相同方法,分别提取交流电流/电压扰动与交流电压/电流响应,就可以通过复阻抗计算公式计算阻抗值啦。以下为车用燃料电池系统上进行阻抗测试的部分数据[2]:
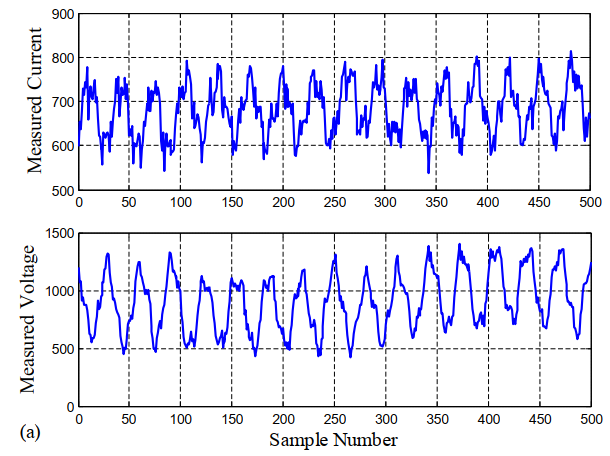
电流与电压信号
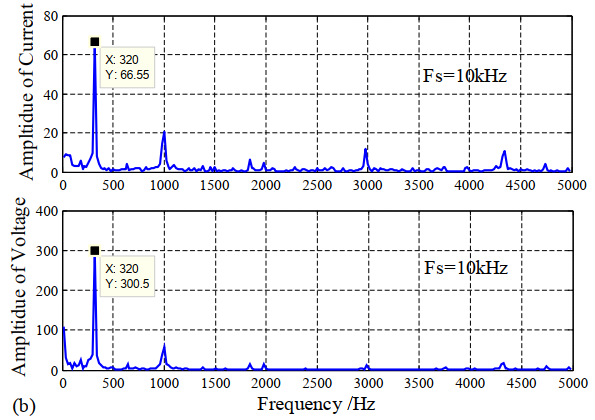
(快速)傅里叶变换后,提取320Hz处的
该过程的原理是相对简单的,但由于阻抗计算对环境相当敏感,在实际测试时,会遇到各种意想不到的干扰,从而影响判断。这就需要我们对阻抗测量手段硬件和软件进行不断投入。
附录
以下部分供参考,后续会重新展开谈谈该部分内容~
快速傅里叶变换(Fast Fourier transform, FFT)
基于稀疏矩阵分解,快速离散傅里叶变换(Discrete Fourier Transform, DFT)或其逆变换的方法。
拉普拉斯(Laplace Transform)变换
从傅立叶变换公式中,我们可以看出,要满足使用条件,要求$f(t)$的柯西主值积分应该是有限值。但是,并非所有信号都满足该条件,可能导致积分发散。
为使得任何信号函数都可积分,可以在傅立叶变换公式中引入衰减因子$e^{\sigma t}$,有
令$s = \sigma - 2 \pi \omega i$,可得到拉普拉斯变换:
其中,$s=\sigma+i \nu$为任意复数。从这个角度来看,拉普拉斯变换是为了对某些不可积函数进行的傅立叶变换的拓展。
Z变换
傅立叶变换的离散形式。
参考文献
[1] Yuan X Z, Song C, Wang H, et al. Electrochemical impedance spectroscopy in PEM fuel cells: fundamentals and applications[J]. 2010.
[2] Hong P, Xu L, Jiang H, et al. A new approach to online AC impedance measurement at high frequency of PEM fuel cell stack[J]. international journal of hydrogen energy, 2017, 42(30): 19156-19169.