交流阻抗谱学的优势在哪？

我们一般更常用的电势阶跃法、线性伏安法和循环伏安法等，都属于暂态分析，即在系统的非稳态下进行分析。交流阻抗谱学（Electrochemical impedance spectroscopy, EIS）是一种在系统稳态下进行分析（稳态分析）的方法，具有高精度（相对）、简化分析和可分析系统长时表现的特点，一定程度上弥补了暂态分析的不足。

交流阻抗分析的主要思想是将复杂的电化学系统简化为一定的等效电路，通过电信号的输入输出对比，基于电工学探知其内部结构的具体参数。

本文所涉及理论内容十分丰富。
博主水平有限，暂时不能一次全部覆盖，将会持续修补更新。
望各位读者批评指正！

本文思路及主要内容均来源于Bard老爷子的《Electrochemical methods: Fundamentals and applications》[1]。

电化学系统中的等效电路

交流阻抗分析的核心正在于此。若将整个电化学系统（电极、电解质、隔膜、电极片等）视作一个灰盒（介于黑盒与白盒之间），通过输入已知信号，得到一定的输出信号，便可印证灰盒中是否存在之前假定的电路元件。同时，在理想情况下，可以通过拟合，实现对电路元件具体参数的测定。

构成电化学系统的基本元器件

物理元器件：电阻、电容、电感（以及，第四类基本电子元器件：忆阻器。新兴领域，非教科书观点。可参考相关文章：钱鹤、吴华强团队在基于新型忆阻器阵列的类脑计算取得重大突破。
电化学系统元器件：电容（双电层结构）、电阻（溶液电阻、接触电阻、材料电阻等）、阻抗（= 电阻 + 电容）。

Randles等效电路

如下的Randles电路是常用的一种针对单个工作电极的等效电路。

Randles等效电路

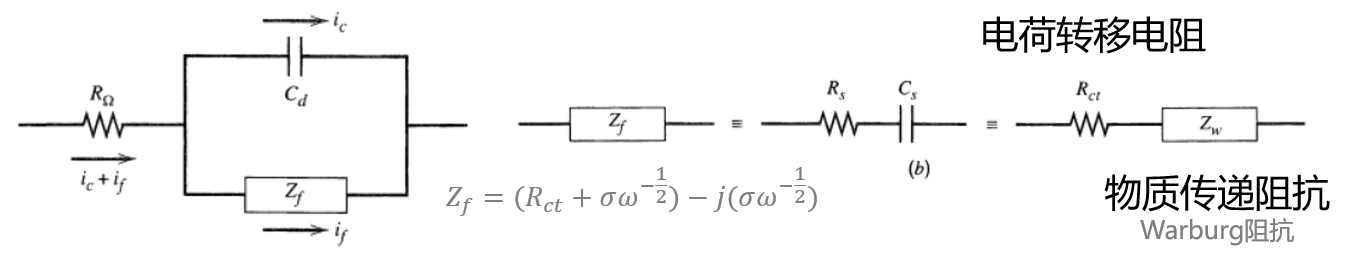
需要注意的是，这里我们说的“等效”与“约等于”不同：“约等于”代表我们可以用数学结构去描述未知的部分，我们甚至有方法去减小这个未知的部分。比如通过Taylor公式我们知道，$x \rightarrow 0$时，$\ln (1+x) \approx x$。这是因为

$\ln(1+x) = x-\frac{x^2}{2}+\frac{x^3}{3}-\frac{x^4}{4}+\cdots$

当$x \rightarrow 0$时，$x^2$、$x^3$及高阶次方$x^n$都趋近于0，于是此时有$\ln (1+x) \rightarrow x$。

“等效”不太一样。我们不清楚电路的具体模型是什么，因此我们假设了一个，对不对我们也不知道。有的时候能够描述比较好，而有的时候不行。因此不代表我们可以用足够复杂的电路去描述一个电化学系统。

但Randles等效电路远非随意假设。在电化学分析中，我们最关注的是化学过程。法拉第过程在电极与电解质之间产生了电子转移，在不同物质之间发生了氧化还原，是我们电化学分析中着重关注的过程。这一过程对应的阻抗即法拉第阻抗$Z_f$，也是我们后来理论推导中的着力点。

电解质电阻与双电层电容

交流信号通过电解质后不发生相位改变，因此其可以简单用一个电阻$R_\Omega$表示。双电层电容指的是由于双电层形成而产生的，类似于物理中双极板电容器的一种化学元器件。受热力学平衡影响，电极浸入电解液后会自动带上电荷，于是在电极-电解质界面的两边，会分别形成所带电荷符号相反的电荷分布。如下图（Stern模型）所示，电极内部带正电荷，电解质中阴离子形成双电层，且阴（阳）离子由于溶剂化而被溶剂分子包裹。

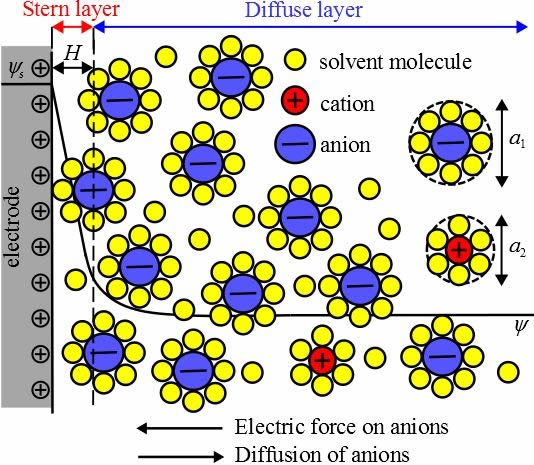
Ref: https://www.seas.ucla.edu/~pilon/EDLCs.htm

有关电荷产生原因的电毛细理论，和双电层电容理论模型，在之前的课后回顾中有所提及，感兴趣的读者可以查看：课后回顾 | 双电层结构。

法拉第阻抗$Z_f$

考虑把法拉第阻抗$Z_f$单独拿出来分析。既然电化学系统中只有电阻和电容两种元器件，那么直观地，阻抗也就可以分解为电阻$R_s$和电容$C_s$的组合。

如果是纯粹物理电路

只有电阻$R_s$和电容$C_s$电路的电压-电流特征是

$E = iR_s + \frac{q}{C_s}$

两边对时间$t$求导

$\frac{\text{d}E}{\text{d}t} = R_s \frac{\text{d}i}{\text{d}t} + \frac{i}{C_s}$

输入正弦交流信号

$i = I \sin (\omega t)$

此处无需考虑电压信号，因此电流信号$i$可以忽略相位差$\phi$，以简化公式。详情可查看附录。

得到等效电路电压特征

$$ \frac{\text{d}E}{\text{d}t} = \left( R_sI\omega \right) \cos(\omega t) + \left( \frac{I}{C_s} \right) \sin(\omega t) $$

回到现实电化学系统

对于一个一般的电化学氧化还原反应

$O + ne^- \rightleftharpoons R$

以下为了清晰显示关系，存在符号的简化。物质浓度均为电极表面浓度，且与电极电势保持同一时刻$t$：
$\begin{split} C_O &= C_O(0, t) \\ C_R &= C_R(0, t) \end{split}$

反应的电极电势$E$与电流$i$、氧化物浓度$C_O$和还原物浓度$C_R$都有关系

$E = f(i, C_o, C_R)$

由电极电势$E$的全微分定义有

$$ \frac{\text{d}E}{\text{d}t} = \frac{\partial E}{\partial i} \frac{\text{d} i}{\text{d} t} + \frac{\partial E}{\partial C_O} \frac{\text{d} C_O}{\text{d} t} + \frac{\partial E}{\partial C_R} \frac{\text{d} C_R}{\text{d} t} $$

再做一个代换，使关系更为清晰

$\frac{\text{d}E}{\text{d}t} = R_{ct} \frac{\text{d} i}{\text{d} t} + \beta_O \frac{\text{d} C_O}{\text{d} t} + \beta_R \frac{\text{d} C_R}{\text{d} t}$

可以得出结论，$\text{d}E / \text{d} t$依赖于等式右边的六个变量

$\begin{split} R_{ct} &= \frac{\partial E}{\partial i} \\ \beta_O &= \frac{\partial E}{\partial C_O} \\ \beta_R &= \frac{\partial E}{\partial C_R} \\ \\i,\quad &C_o,\quad C_R \end{split}$

通过组装$R_s$和$C_s$获得法拉第阻抗$Z_f$

直接对电流信号$i= I \sin (\omega t+\phi)$进行求导可得

$\frac{\text{d}i}{\text{d}t} = I \omega \cos(\omega t)$

基于半无限扩散模型，经过足够长的时间$t$，系统达到稳态，（中间省略部分数学处理）可得

$\frac{\text{d} C_O}{\text{d} t} = \frac{I}{nFA} \left( \frac{\omega}{2D_O} \right)^{1/2} \sin(\omega t) + \cos(\omega t) \\ \frac{\text{d} C_R}{\text{d} t} = \frac{I}{nFA} \left( \frac{\omega}{2D_R} \right)^{1/2} \sin(\omega t) + \cos(\omega t)$

以上三式可带入$\text{d}E / \text{d} t$的描述公式中，简化得到

$$ \frac{\text{d}E}{\text{d}t} = \left( R_{ct} + \sigma\omega^{-1/2} \right) I\omega \cos(\omega t) + \left( \sigma \omega^{1/2} \right) I \sin(\omega t) $$

把之前从纯物理角度得到的电压特征取来

$\frac{\text{d}E}{\text{d}t} = R_s \cdot I\omega \cos(\omega t) + \left( \frac{1}{C_s} \right) I \sin(\omega t)$

可对比得出对应电阻$R_s$和电容$C_s$

$R_s = R_{ct} + \sigma \omega^{-1/2}$ $C_s = \sigma^{-1} \omega^{-1/2}$

通过组装可以得出法拉第阻抗$ Z_f $

$$ Z_f = R_s+ C_s = R_s - j \frac{1}{\omega C_s} = R_{ct} + \sigma \omega^{-1/2}-j(\sigma \omega^{-1/2}) $$

电荷传递阻抗$R_{ct}$和$Warburg$阻抗

回到阻抗分析的方法上来。我们输入的是不同频率的小幅正弦交流电信号，然后观察电化学系统的响应。

小幅是因为$x \rightarrow 0$时，才有$sin(x) \approx x$，对正弦信号的响应与对线性信号响应趋同，从而简化分析。

那么在理论模型上就应该把受频率影响的部分和不受频率影响的部分都单独拎出来。于是有了如下的写法，

电荷传递阻抗

$R_{ct}$

Warburg阻抗（与传质相关）

$\sigma \omega^{-1/2}-j(\sigma \omega^{-1/2})$

电化学系统总阻抗

总阻抗为负数，因此可分为实部和虚部

$Z = Z_{Re} + Z_{Im}$

（中间省略部分数学处理）且

$Z_{Re} = R_\Omega + \frac{R_{ct} + \sigma \omega^{-1/2}} {(C_d \sigma \omega^{1/2})^2 + (R_{ct} + \sigma \omega^{-1/2})^2}$ $Z_{Im} = \frac{\omega C_d (R_{ct} + \sigma \omega^{-1/2}) + \sigma \omega^{-1/2} (\omega^{1/2} C_d + 1)} {(\sigma\omega^{1/2} C_d + 1)^2 + \omega^2 C_d^2(R_{ct} + \sigma \omega^{-1/2})^2}$

低频极限，$\omega \rightarrow 0$

$Z_{Im} = Z_{Re} - R_\Omega - R_{ct} + 2 \sigma^2 C_d$

对应Nyquist图如下

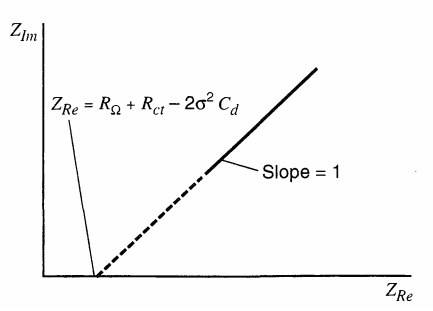
理想情况下，这应该是一条斜率为1的直线，与$Z_{Re}$轴的交点为$(R_\Omega - R_{ct} + 2 \sigma^2 C_d, 0)$。

高频极限，$\omega \rightarrow \infty$

$\left( Z_{Re} - R_\Omega - \frac{R_{ct}}{2}\right)^2 + Z_{Im}^2 = \left( \frac{R_{ct}}{2} \right)^2$

对应Nyquist图如下

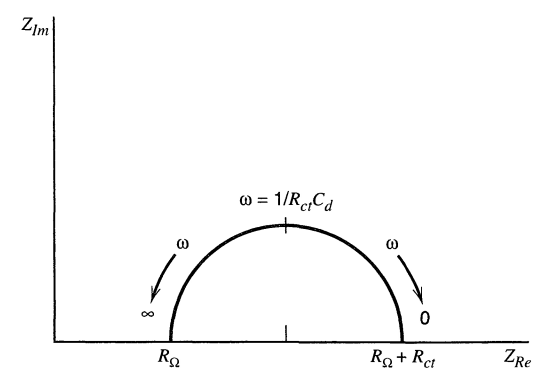
理想情况下，这应该是一个圆心为$(R_\Omega + \frac{R_{ct}}{2}, 0)$，半径为$\frac{R_{ct}}{2}$的半圆。

现实阻抗在两个极限情况之间

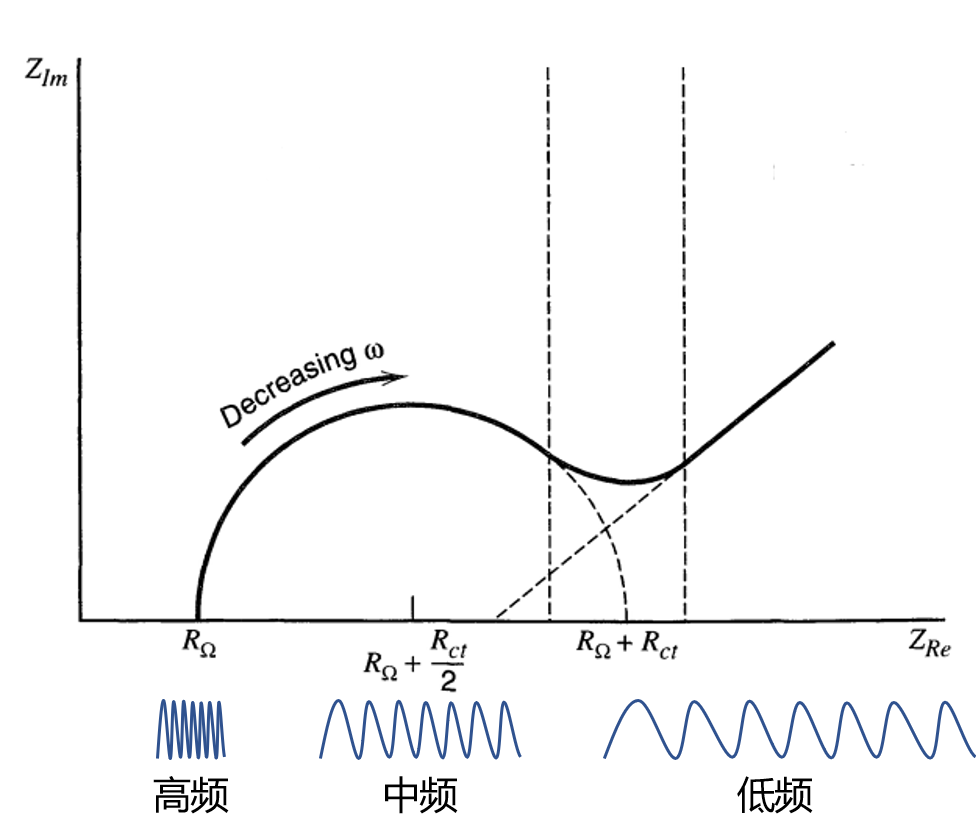
中频部分是高频与低频阻抗谱的过渡，以圆弧连接。因此Randles等效电路对应的Nyquist图一般呈如下形状

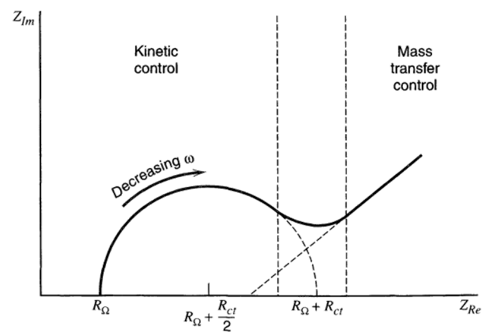
另外，可通过基于最小二乘法等优化方法的软件可对其进行拟合，从而得到具体的电化学系统元器件参数。拟合软件有ZSimDemo等。

在能源电化学中的应用实例

在能源电化学中常用的结论有以下几个：

从以上Nyquist图中不难看出，高频区域的半圆与$R_{Im}$的交点为电解质阻值$R_\Omega$，而其直径为$R_{ct}$[1, 2]。也就是说，半圆直径越小，电子转移阻抗越小，一般也越有利于电化学反应的发生。

为什么说一般呢？要是存在选择性问题，电子转移阻抗对反应电化学活性的影响就可能不同了。

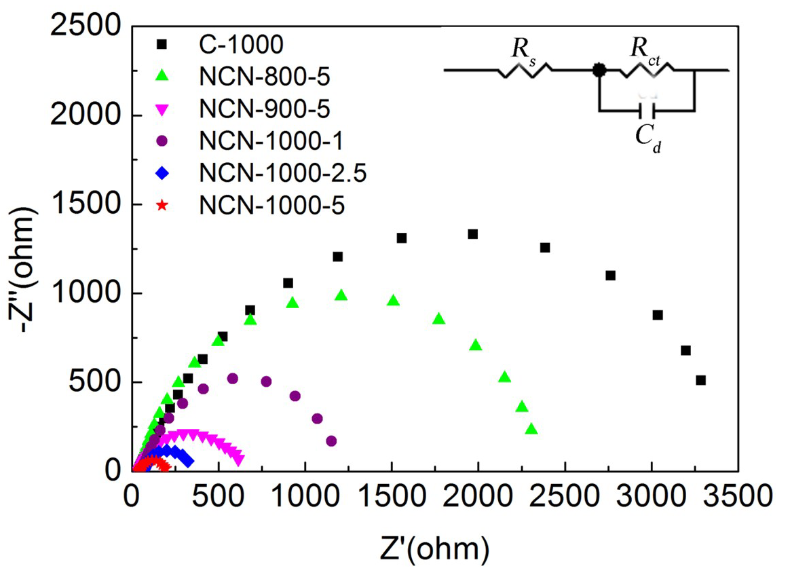
Ref: Jiang et al. Defect-Rich and Ultrathin N Doped Carbon Nanosheets as Advanced Trifunctional Metal-Free Electrocatalysts for the ORR, OER and HER. Energy Environ. Sci. 2019, 12 (1), 322–333.

低频区域直线的的斜率与离子扩散系数呈线性关系，反映了离子传输阻抗：斜率越大，离子扩散系数越大[3]。

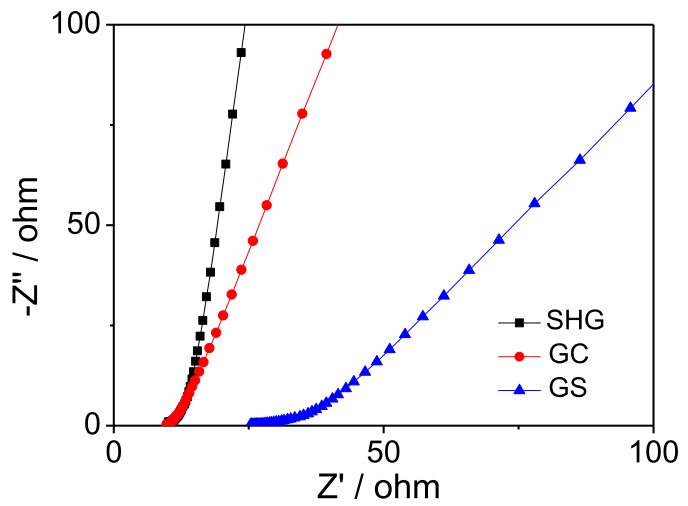
Ref: Dai* et al. Multifunctional Carbon-Based Metal-Free Electrocatalysts for Simultaneous Oxygen Reduction, Oxygen Evolution, and Hydrogen Evolution. Adv. Mater. 2017, 29 (9), 1604942.

高频和中频区域可能出现两个半圆。其中前一个半圆（高频）对应钝化膜形成阻抗（passivated film impedance），后一个半圆（中频）对应电荷转移阻抗（charge-transfer resistance）[4]。这种半圆或圆弧的数目与等效电路中的电容个数直接相关[2]。

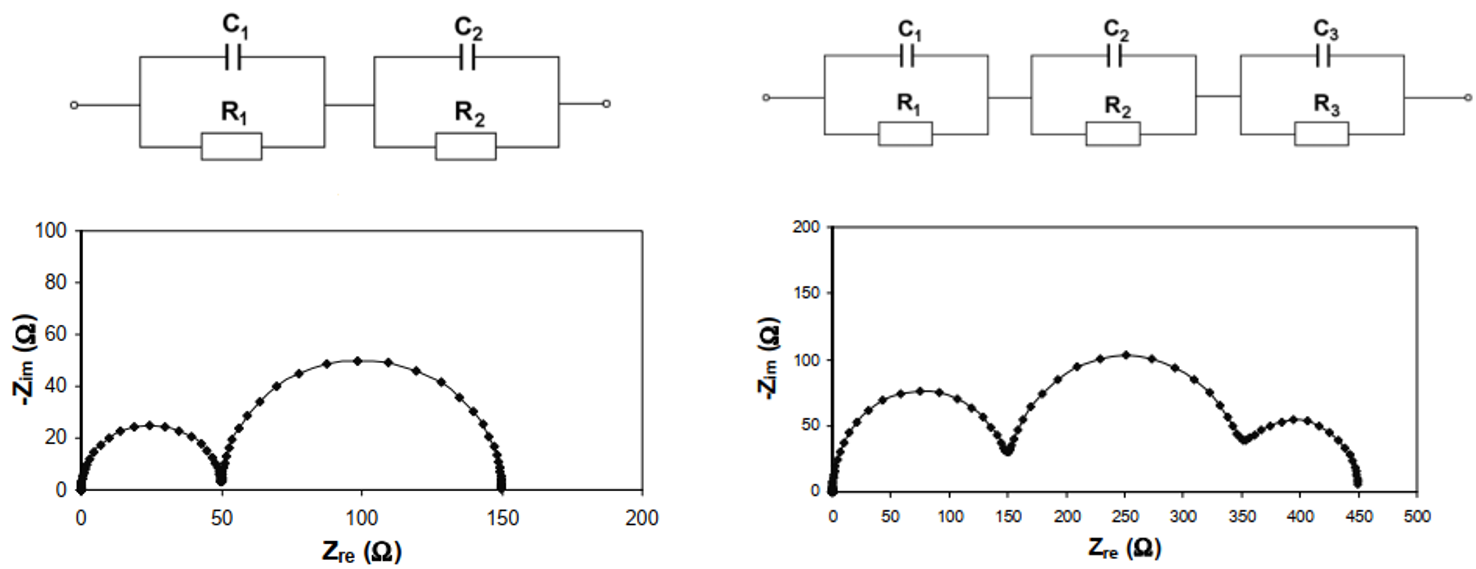
Ref: Yuan et al. Electrochemical Impedance Spectroscopy in PEM Fuel Cells; 2010.

参考文献

[1] Bard, A. J., Faulkner, L. R., Leddy, J., & Zoski, C. G. (1980). Electrochemical methods: Fundamentals and applications (Vol. 2). New York: wiley.

[2] Yang, X.; Rogach, A. L. Electrochemical Techniques in Battery Research: A Tutorial for Nonelectrochemists. Adv. Energy Mater. 2019, 9 (25), 1900747.

[3] Dai* et al. Multifunctional Carbon-Based Metal-Free Electrocatalysts for Simultaneous Oxygen Reduction, Oxygen Evolution, and Hydrogen Evolution. Adv. Mater. 2017, 29 (9), 1604942.

[4] (a) Mirzaeian M, Hall P J. Characterizing capacity loss of lithium oxygen batteries by impedance spectroscopy [J]. J Power Sources, 2010, 195: 6817-6824.(b) Song J Y, Lee H H, Wang Y Y, et al. Two- and three-electrode impedance spectroscopy of lithium-ion batteries [J]. J Power Sources, 2002, 111: 255-267. (c) Chang Y C, Sohn H J. Electrochemical impedance analysis for lithium ion intercalation into graphitized carbons [J]. J Electrochem Soc, 2000, 147: 50-58.

附录

电阻

假设一个正弦电压信号

$e = E \sin (\omega t)$

与其对应的电流信号往往会与电压信号存在一定相位差$\phi$

$i=I \sin(\omega t + \phi)$

在恒电位仪上，我们可以对只含一个阻值为$R$的电阻施加正弦电压信号，此时Ohm定律$E=IR$和$e=iR$一直成立，于是有

只在纯电阻电路中Ohm定律总是适用。

$e = RI \sin(\omega t) = Ri = RI \sin(\omega t + \phi)$

即此时电压信号$e$和电流信号$i$的相位差$\phi$为0。

电容

施加正弦电压信号$e = E \sin(\omega t)$通过一个电容值为$C$的纯电容，根据电容定义$q=Ce$，两边对$t$求导

$i = \frac{\text{d} q}{\text{d} t} = C \frac{\text{d} e}{\text{d} t} = \omega CE \cos(\omega t) = \omega CE \sin(\omega t)$

考虑容抗后，Ohm定律$e=iR$仍成立

$i = \frac{e}{Z_C} = \frac{E}{Z_C} \sin \left( \omega t + \frac{\pi}{2} \right)$

其中容抗$Z_C = \frac{1}{\omega C}$。此时可以对比出电压信号$e$和电流信号$i$的相位差$\phi$为$\frac{\pi}{2}$。