
之前我们说到,如何将LAMMPS正常运行,并对LAMMPS的in文件和输入文件进行修改调试,查看结果。可以说,基本与科学无关,纯属dirty work。但科学也是在dirty work的基础上架构的。
这一次,我们准备触及分子动力学的中的物理内核。
分子动力学是什么?
先给出Wikipedia的定义[1]:
Molecular dynamics (MD) is a computer simulation method for analyzing the physical movements of atoms and molecules.
博主的理解是,分子动力学(Molecular dynamics)是以一个原子为最小单元,基于经典牛顿力学原理,对整个系统的原子/分子运动状态进行模拟的一套理论。由于整套理论的基础是牛顿力学,所以其适用范围也就不言自明了——相对论或者量子理论作用不可忽略的有关性质,利用分子动力学模拟是无法得到合理结论的。幸运的是,分子热运动的速度< 1000 m/s,远小于光速[2];部分性质如力学性质中,电子转移对原子/分子的运动影响较小。除了近年来研究较多的电子转移,其实很多传统领域(如材料形变、蛋白质分子折叠等)使用分子动力学都不算超纲。
如何利用分子动力学?
每个原子所受作用主要分为化学键作用和非键作用。
这些作用都利用势函数(能量函数)来进行描述。
势函数(Potential)
以下是大学物理中可以见到的原子间作用势的基本形状:
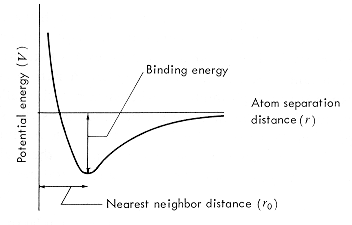
Ref: https://www.princeton.edu/~maelabs/mae324/glos324/potential.htm
出现这种曲线的原因是
吸引力与排斥力方向相反,符号相反。
无穷远处吸引力与排斥力均趋近于0;随着两原子靠近,原子间的吸引力开始气作用;突破平衡距离$r_0$后,排斥力的作用开始逐渐增大,阻止两原子继续靠近。
此即
将原子在无穷远处的系统能量定义为0,系统能量增加全部由做功所提供。将原子距离从无穷远缩短为$r$的这段过程中,原子做功为
即等于两原子间内能。将原子间作用力两两加和便可达到由$N$个原子组成系统的内能。当不考虑物体外力场的作用时,由$N$个原子组成系统的总能量也就等于系统内能:
需要注意的是,为排除重复计算的原子间作用力,需要加上系数$\frac{1}{2}$。以上就是原子间作用力计算系统内能的基本原理。
化学键作用$E_{bond}$
谐振子势(Harmonic)
$$ \begin{split} E_{stretch} &= K_{stretch} (r-r_0)^2 \\ E_{bend} &= K_{bend} (\theta-\theta_0)^2 \\ \end{split} $$
其中$r-r_0$和$\theta-\theta_0$即为分子间伸缩运动和弯剪运动偏离平衡的量,$K_{stretch}$和$K_{bend}$都是常数。“Harmonic”指的应该是“Harmonic oscillator”,以下是Wikipedia的定义[3]:
谐振子(Harmonic oscillator)
In classical mechanics, a harmonic oscillator is a system that, when displaced from its equilibrium position, experiences a restoring force $\vec{F}$ proportional to the displacement $\vec{x}$:
即遵循Hooke定律的系统,可称为谐振子。由力与能量的关系,不难得:
其中,$k$为弹簧系数,$x$为偏离平衡的位移。这也就是Harmonic势中的公式形式。
非键作用$E_{non-bond}$
分子动力学模拟使用力场实现对每个原子所受作用的计算。力场就是通过一定的函数,在所有原子之间,计算两两原子之间的相互作用力。这其中主要包括范德华力(Van der Waals force)、静电作用力(Coulomb force)等。
静电作用力
静电作用力与高中课本中描述的没有差异。原子$i$和原子$j$间的静电作用力为
范德华力
两体势(Pair potential)
广泛应用的两体势是Lennard-Jones(L-J)势,在描述Ar, Kr, CH4, O2, H2, C2H4等小分子的范德华力方面具有明显优势[4]。原子$i$和原子$j$间的范德华力为
$$ E^{LJ}_{ij} = 4 \epsilon \left[ \left( \frac{\sigma_{ij}}{r} \right)^{12} - \left( \frac{\sigma_{ij}}{r} \right)^{6} \right] $$
为了节省计算资源,两体之间的势都有截断能。引入截断能(cut off)$r_C$后,原子$i$和原子$j$间的范德华力为
使用lj/cut势并设定参数:
1 | pair_style lj/cut 2.5 |
其中2.5为截断能。pair_coeff共有5个参数,前两个参数指定原子类型,后三个参数指定势函数参数。
若将静电作用力(也考虑截断能)也考虑进来,可选择lj/cut/coul/cut:
1 | pair_style lj/cut/coul/cut 10.0 8.0 |
其中10.0为L-J势的截断能,8.0为静电作用力力的截断能。
多体势
Baskes和Daw基于密度泛函理论和准原子近似理论,导出了嵌入原子理论(embedded atom method, EAM)模型势[5]。该势函数是目前描述金属及其合金原子间作用最有效的,几乎适用于任何金属元素及合金。唯一的问题是势函数的参数需要拟合确定。
$$ E_{EAM} = \sum_i \left\{ F_i(\rho_i) + \frac{1}{2} \sum_{i \neq j} \phi_{ij} (r_{ij}) \right\} $$
在LAMMPS中,对应EAM势的势函数为eam势:
使用eam势:
1 | pair_style eam |
通过library.meam设置势函数参数:
1 | pair_coeff * * cuu3 |
在LAMMPS中还有一个常用的多体势。mean势——Modified Embedded-atom Method (MEAM)。“Modified”的部分在于相对EAM,MEAM还加入了键角的作用(angular forces)。据LAMMPS官方文档描述,在2018年12月的版本后,mean势被替换为mean/c。二者基本可以等效,但mean/c要更为高效[5]。
使用mean/c势:
1 | pair_style meam/c |
通过library.meam设置势函数参数:
1 | pair_coeff * * ../potentials/library.meam Ni Al NULL Ni Al Ni Ni |
写在后面
以上博主对LAMMPS的介绍还只是LAMMPS的冰山一角。
如果恰好引起了你的兴趣,请到LAMMPS官网查看相关文档。
博主只希望本系列文章能够让更多自然科学与实验科学的同学关注对应的计算与信息方向。
三百六十行,行行信息化。
我相信,利用信息技术可以让传统学科焕发出新的活力,并呈现出无限可能。
参考资料
[1] https://en.wikipedia.org/wiki/Molecular_dynamics.
[2] https://en.wikipedia.org/wiki/Thermal_velocity.
[3] https://en.wikipedia.org/wiki/Harmonic_oscillator.
[4] The Journal of Chemical Physics 104:21, 8627-8638.
[5] Daw, Baskes, Phys Rev Lett, 50, 1285 (1983). Daw, Baskes, Phys Rev B, 29, 6443 (1984).