设计 / 思考 / 材料 / 信息

0%

遗传算法 | 展馆安全保障问题

发表于 更新于 分类于 Valine：

关键词：摄像头、组合优化、遗传算法

原题目及其分析

首先，放上完整的题目，如下所示。

你们保安公司与某艺术展馆签订了一项安保合同，为他们安装摄像监视装置。由于这些摄像装置较大，会对展馆参观者视线形成干扰，所以展馆管理方希望这些装置安装得越少越好，并且希望摄像机尽可能装在角落处。
摄像机当固定摄像时能清晰分辨的距离为7.5米，当水平旋转摄像时能清晰分辨的距离为2.5米，摄像头视角大约为50度。
多数展馆都希望最大限度地利用空间展示展品，所以展馆的平面布局相当复杂，有一些隔板会以各种角度立在房间中间或者走廊上。尽管该展厅很大（见图1、图2），但任何两个对面墙之间的距离并不大，所以参观者不需要无谓地走很多路。所有的墙壁以及隔板都是平的。

  1. 主要任务：你们的任务是为固定或可转动摄像机设计安装位置，以期在夜晚能够提供尽可能多的覆盖面积，包括地面与墙壁展示区域。
  2. 资金拮据问题：由于预算资金不足，不能在全馆安装足够数量的监视摄像机，试讨论这种情形下的最优安装策略，并给出相应的安全性评价。

看完题目后，第一步我们需要分析题目给我们提出的两个问题是什么性质的问题。

主要任务：你们的任务是为固定或可转动摄像机设计安装位置，以期在夜晚能够提供尽可能多的覆盖面积，包括地面与墙壁展示区域。

从题中可以清晰看出，“尽可能多”意味着这本质上是一个优化问题。而优化问题的本质可以解释为，在可选策略中找到一个最好的，实现优化目标值的最大化。

这是什么意思呢？

以上题为例。安装摄像头的种类，以及我们选择安装在什么位置，是我们可选的策略。在这些策略中，显然会出现监视覆盖面积的不同，这是由摄像头的物理本质所导致的。而题目后半部分提出，要使得覆盖面积最大化，即取一个摄像头安装方案，与其他的安装方案相比，能够获得最大的监视覆盖面积。

由以上分析，我们不难想到，如果我们能够把所有的安装方案都罗列并充分计算，然后比较各方案的监视器覆盖面积，岂不是很轻易就解决了问题？

在这里，问题不如想象那么复杂，却也没有那么简单。要实现这个优化算法，我们需要克服以下几个困难：

  1. 将所有摄像头安装策略量化。这一步是数学建模的基础，没有量化的生活问题是没法建立模型进行计算的。
  2. 考虑到这样的问题难以实现解析的描述，我们还需要实现决策的离散化，即把安装策略控制在有限个数内。这样的话，问题规模足够小的情况下，我们甚至是可以通过暴力穷举来进行求解的。
  3. 问题规模较大时，穷举法将不适用。这时我们需要另辟蹊径，或许可以求助与大规模离散优化算法中的智能算法。

接下来的解题过程中，我们需要一步步依次解决以上三个问题。这其实也是大多数优化类型题目的解题套路。本文着重介绍如何使用遗传算法（GA，Genetic Algorithm）。至于遗传算法思路，在本文不做详细介绍，感兴趣的同学可以自行查找相关资料。

资金拮据问题：由于预算资金不足，不能在全馆安装足够数量的监视摄像机，试讨论这种情形下的最优安装策略，并给出相应的安全性评价。

如果只是求摄像头监视覆盖面积的最大化，其实是不符合实际的。因为我们只需增加摄像头的个数，便可以毫无疑问地提高监视覆盖面积。因此，有可能是资金受限，有可能是摄像头种类或者个数受限，总之必需对摄像头施加一定约束才可以使问题更贴近于实际。这也是题目中第二点要求给我们提出的要求。

在最后，题目还要求我们做出“安全性评价”。由于这个“安全性”这个名词没有任何严格定义，实际上我们能够选择任何我们喜欢的指标进行评价，例如监视覆盖面积（很明显）、地面覆盖面积、单位时间覆盖面积等等。

题目分析基本完成以后，就可以开始以下的解题过程了。

解题过程

摄像头模型分析

题中给出摄像头的两种安装方式：固定式安装和旋转式安装，其中固定式安装清晰分辨的距离为7.5米，旋转式安装清晰分辨的距离为2.5米，两种方式摄像头视角大约为50°。由题意得固定式摄像头的监控为一个顶角为50°，母线长为7.5m的圆锥和半径为7.5m的球壳围成的区域，旋转式摄像头的监控范围为一个半径为2.5m的半球壳被一个同旋转中心的顶角为50°，母线长2.5m的圆锥截剩下区域。假设监控设备水平安装，在距固定式摄像头垂直距离不超过5.74m，距旋转式摄像头垂直距离不超过1.92m的一水平高度上两者监视范围分别为监视区域的一个水平截面。
由于摄像头尽量安装在角落处，固定式摄像头有效监视区与墙壁及临近摄像头有效监视区可将监视盲区包围，旋转式摄像头自身监视盲区被有效监视区包围，参观者无法避过监视区域到达监视盲区，可将该盲区视为安全范围，因此可将两者的三维监视区域二维化，简化为其监视区域在水平面上的投影，即一个顶角为50°，半径为7.5m的扇形和一个半径为2.5m的圆。如下图所示：

摄像头监视范围示意图

摄像头安装策略

样本制作（从0到1）

为了将“所有摄像头安装策略量化”，我们想到的方案是，人工筛选摄像头安装方案的样本。这样做不仅使得安装策略变成了简单的安装方案的简单叠加，还使得安装策略个数限制在了有限个数内，效果如下图所示：

整个制作过程主要依赖Photoshop 2014cc版本进行完成，这其中，当然不可避免的会掺杂主观因素——至少基本的摄像头安装方案样本是我们主观选取的。可以想象，选取的基本样本不同，对最后的安装方案也会有一定影响。但是，这些问题在数学建模这个大背景下显得不是那么重要，我们需要做的就是大胆想象，并客观地分析模型利弊。

具体地，三个展厅分别的基础样本展示如下：

Challenge of Modern Art Interactive Gallery摄像头安装方案样本

South Gallery & North Gallery摄像头安装方案样本

Permanent Exhibition Area摄像头安装方案样本

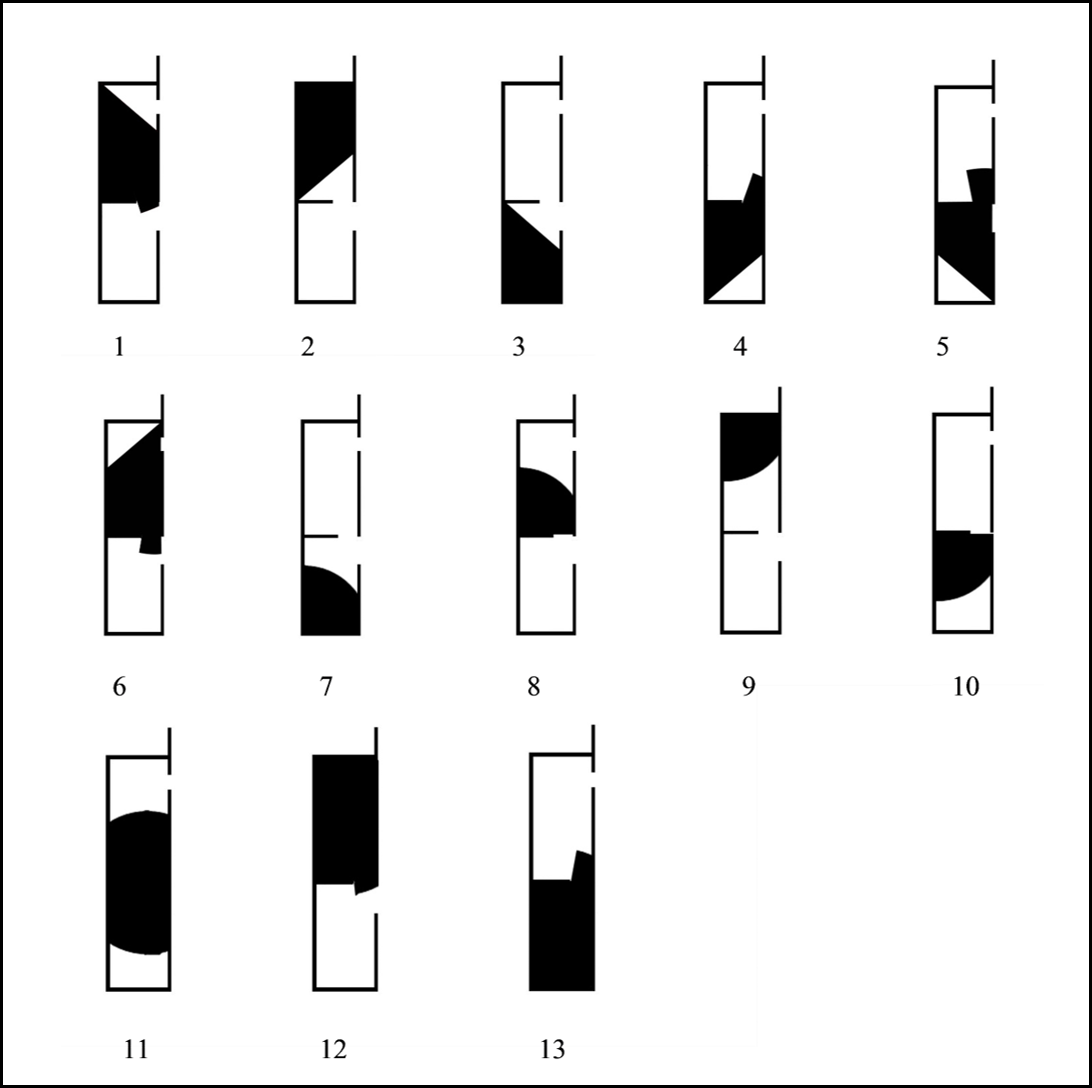
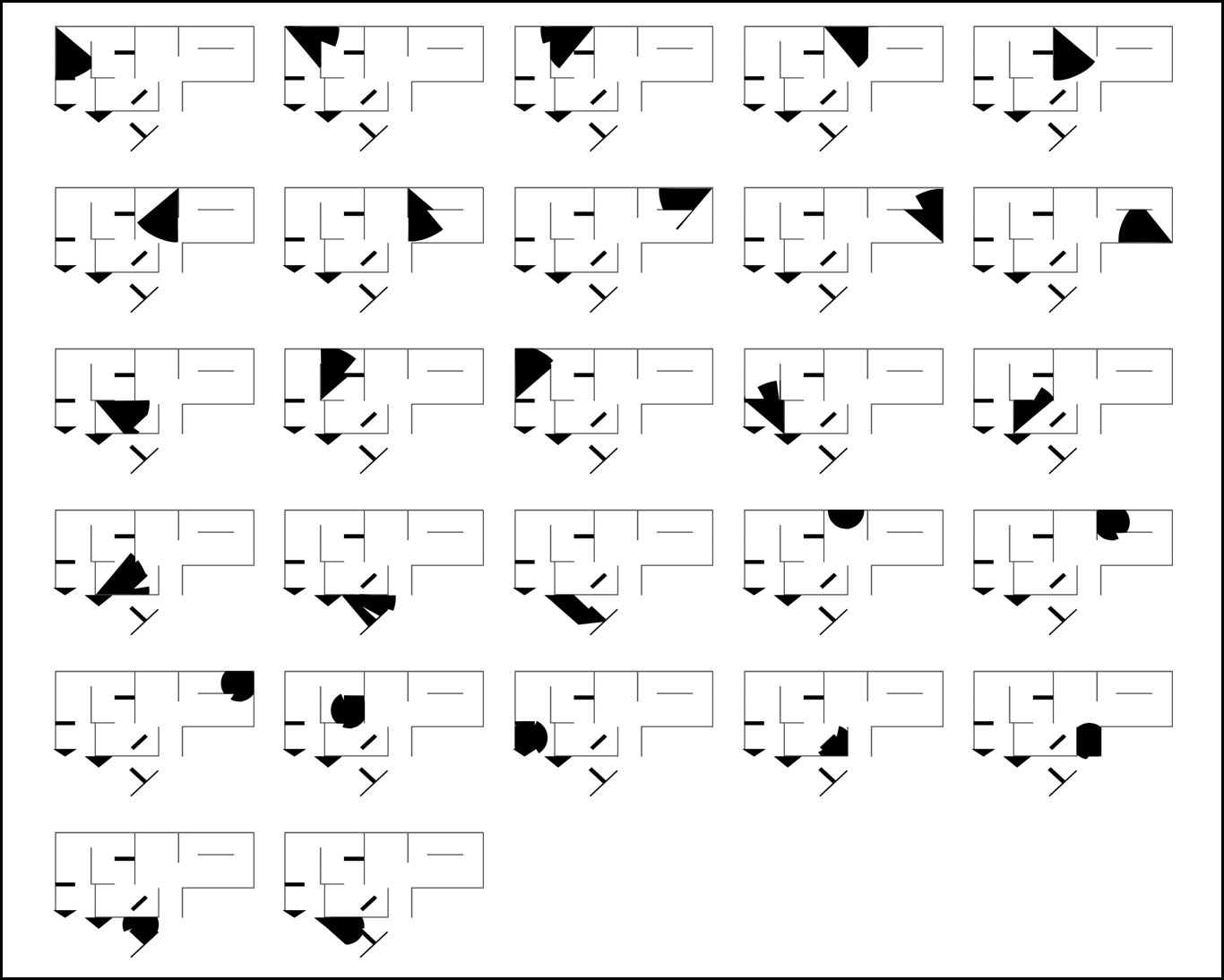
样本叠加（从1到n）

得到图片样本后，我们还需将图片读入MATLAB进行处理。这主要依赖MATLAB提供的图片信息读取函数imread解决。而为了提高图片运算速度，我们还需要将图片信息二值化。

JPG图片信息导入MATLAB后，是一个二维矩阵。矩阵上的每一个点包含三个值，即RGB的颜色信息。二值化就是把RGB信息变成0或者1，这样整个图片信息矩阵可以变成一个纯粹逻辑矩阵，叠加运算的速度可以加快很多。这样的处理是有意义而必要的。

根据上述逻辑，

图片叠加 = 逻辑矩阵叠加 = 逻辑矩阵1 + 逻辑矩阵2 + … 逻辑矩阵n

因此，我们通过图片处理得到逻辑矩阵后，就可以实现安装策略的充分定义了——安装策略 = 基本安装方案的简单叠加。至此，我们已经可以估计各个待监视区域摄像头安装方案解空间的大小了：

Challenge of Modern Art Interactive Gallery选取了15个基本样本，其解空间大小为$2^{15}$；

South Gallery & North Gallery选取了13个基本样本，其解空间大小为选取了13个基本样本，其解空间大小为$2^{13}$；

Permanent Exhibition Area选取了13个基本样本，其解空间大小为$2^{27}$。

监视区域覆盖面积

穷举法求解

以上模型有一个缺陷，当然也应该是题目要求的缺陷。

很明显，摄像头个数越多，那么监视区域覆盖面积就会越大。在这里，本文定义了摄像头的单位覆盖面积为“监视区域覆盖面积/摄像头总个数”。从而可以达到一个比较好的符合实际的优化结果。

通过上机进行穷举实验，我们发现，$2^{13-15}$的解空间是可以利用穷举法求解的，即对各基础样本进行叠加实验，试出最大的监视区域覆盖面积。很顺利的，笔者通过两次穷举方法求解出了最佳安装方案（最大的摄像头单位覆盖面积），可参见本文最后图中结果。

遗传算法求解

而$2^{27}$的解空间大小则不能通过简单的穷举方法进行求解。因此，考虑使用遗传算法对Permanent Exhibition Area的安装方案进行优化求解。

在下面，由于空间所限，笔者暂时只讲核心算法——遗传算法代码（使用MATLAB编写）列于下方。需要声明的是，本段代码设计参考并修改自网络上的开源代码，如有侵权，请联系本人删除。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
% 二进制编码遗传算法求解
clc;
clear all;
close all;
% 主程序中声明global，子程序可调用
global BitLength
global boundsbegin
global boundsend
%% 算法初始状态设置
bounds=[0 1];%一维自变量的取值范围
precision=1e-4; %运算精度
boundsbegin=bounds(:,1);
boundsend=bounds(:,2);
BitLength=27;
popsize=50; %初始种群大小
Generationnmax=20;  %最大代数
pcrossover=0.60; %交配概率
pmutation=0.02; %变异概率
%% 主程序
%产生初始种群，摄像头个数在9个以上
while(1)
    population=round(rand(popsize,BitLength));
    if sum(population)>9
        break;
    end
end
%计算适应度,返回适应度Fitvalue和累积概率cumsump
[Fitvalue,cumsump]=fitnessval(population);  
Generation=1;

% 循环终止条件为达到最大代数，在机时较充裕时可设置达到误差精度后终止
while Generation<Generationnmax+1
    str=strcat('目前是第',Generation,'代！');
    disp(str)
   for j=1:2:popsize 
      %选择操作
      seln=selection(population,cumsump);
      %交叉操作
      scro=crossover(population,seln,pcrossover);
      scnew(j,:)=scro(1,:);
      scnew(j+1,:)=scro(2,:);
      %变异操作
      smnew(j,:)=mutation(scnew(j,:),pmutation);
      smnew(j+1,:)=mutation(scnew(j+1,:),pmutation);
   end
   population=smnew;  %产生了新的种群
   %计算新种群的适应度   
   [Fitvalue,cumsump]=fitnessval(population);
   %记录当前代最好的适应度和平均适应度
   [fmax,nmax]=max(Fitvalue);
   fmean=mean(Fitvalue);
   ymax(Generation)=fmax;
   ymean(Generation)=fmean;
   %记录当前代的最佳染色体个体
   xmax(Generation)=Room1Search(population(nmax,:));
   Bestpopulation=population(nmax,:);
   Generation=Generation+1;
end
%% 结果显示
Generation=Generation-1
Besttargetfunvalue=Room1Search(Bestpopulation)
Bestpopulation
hand=plot(1:Generation,ymean);
set(hand,'color','r','linestyle','-','linewidth',1.8,'marker','h','markersize',6)
xlabel('进化代数');ylabel('最大/平均适应度');xlim([1 Generationnmax]);
legend('最大适应度','平均适应度');
box off;hold off;

求解结果

最后最优方案的覆盖示意图：

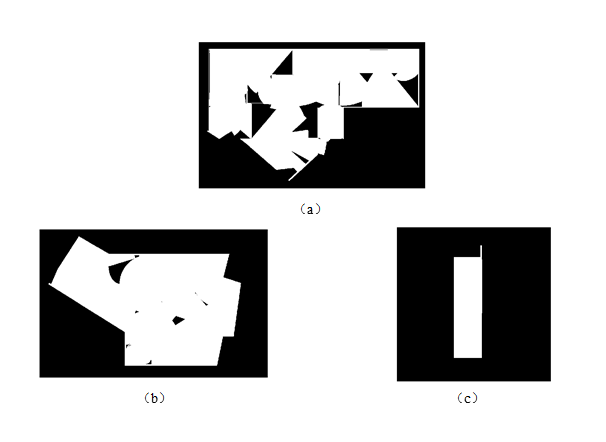
三个展馆最优方案的MATLAB二值化覆盖示意图 (a) Permanent Exhibition Area (b) Challenge of Modern Art Interactive Gallery (c) South Gallery&North Gallery

至此，本文已经搭建了一个摄像头安装方案的较完整的解决思路框架。