写在前面

宏观模型（Macroscopic Model）主要通过热力学方法，对化学反应中的动力学过程进行讨论。其中过渡态理论是对Arrhenius公式所进行的完善，Butler-Volmer公式是利用以上规律对电流电压关系的求解，而Marcus-Hush理论是对以上所考虑的电子传递过程的更复杂化（溶剂化）的考虑。接下来，笔者会对四个模型的核心思想进行简要介绍。

模型讨论

Arrhenius公式

$K = A \cdot e^{-\frac{E}{k_{B}T}} = A \cdot e^{-\beta E}$

热激活过程几乎均适用的经验公式。该公式的缺点在于不能解释指前因子的物理含义。

在一定电化学系统中，指前因子的对数与活化能成线性关系。该现象被称为补偿效应（Compensation Effect）。

过渡态理论（TST, Transition State Theory）

通过合理假设，赋予指前系数以物理意义。

$K = \frac{k_{B}T}{h} \frac{Q^{TS}}{Q^{reaction}} e^{-\beta \Delta E}$

难点：配分函数（统计热力学概念）的理解，在文首所标识的PDF文件中做了详细阐述，感兴趣的读者可前去查看。

Butler-Volmer公式

电化学反应动力学中，最早提出，并且仍然应用最广泛的公式。主要思想为增加电势$\eta$前后，自由能曲线会发生变化，如文献[2]中图示。

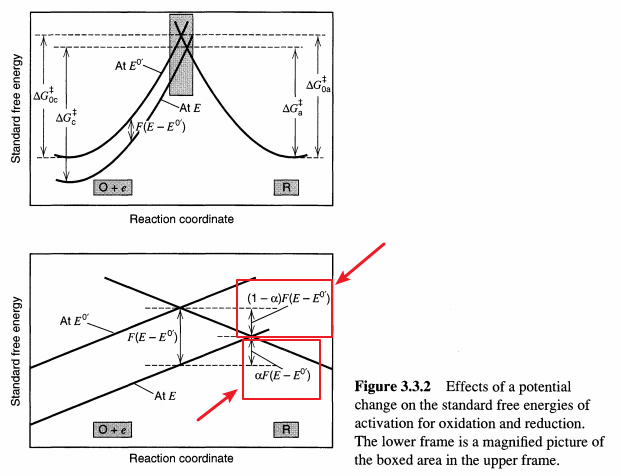
图中，$\eta = E-E_{0}$. 增加电势$\eta$前

$r=k_{+}c_{ox}-k_{-}c_{red}$

增加电势$\eta$后

$r=k_{+}^{0}exp(-\frac{\alpha F \eta}{RT})c_{ox} - k_{-}^{0}exp(-\frac{(1-\alpha) F \eta}{RT})c_{red}$

Marcus-Hush理论

考虑离子溶剂化实体的振动对反应活化能的影响。
始态离子处于氧化态，其能量为

$E_{ox}=\frac{1}{2}x^{2}+gx$

终态离子处于还原态，其能量为

$E_{red}=\frac{1}{2}x^{2}+E_{e}$

令重组能$\lambda=\frac{1}{2}g^{2}$，溶剂化坐标$q=\frac{E_{e}}{2\lambda}$，则可得到Marcus-Hush理论关于活化能的简单表达形式

$E_{a}=\frac{(E_{e}+2\lambda)^{2}}{4\lambda}$

有关于Marcus-Hush理论的复杂表达形式可查看Marcus的原始文献。

参考材料

[1] 何政达. LectureNote of Electrochemistry. 2017.
[2] Bard A J, Faulkner L R, Bard A, et al. Electrochemical Methods: Fundamentals and Applications, 2nd edn[M]. Wiley, 2001.