Why are we interested in this?
These days I knew something called “Gimbal”, which offsets random movements of camera when we are videoing or shooting, in order to make smoother video. It acts like this

Also, several days before, we carefully analyze divers’ physics during diving.
So, em… I think, we can bring those two together, to achieve a deeper understanding of the physics behind gimbal or diving. OK, let’s get started.
Here we start!
Basis of momentum
According to Newton’s Second Law (in a vector form), we have
Impulse is the gain of force along time direction. According to Momentum Theorem, impulse equals to change of momentum, that means, they share the same unit. Then we have
It is similar that, angular momentum system obeys the same rule
where $\vec{L}$ is the angular momentum of the system, I is the rotational inertia of the system, $\vec{\beta}$ is the angular acceleration of the system, $\vec{\Omega}$ is the angular velocity of the system. The angular velocity can be rewrite as
$$ \vec{\Omega}=I^{-1}\vec{L} $$
Relation above is vital important, and we will use it later.
In a “free” rigid body system
In a rigid body system, L is described as a moving vector, and its length $l$ remains constant. We construct a rotation matrix $R \in SO(3)$ which do the transformation of $\vec{l}=R\vec{L}$ and always maintain $|\vec{l}|$. To derive the equation of motion for rigid body, we take the time derivative of $\vec{l}=R\vec{L}$, which gives
That’s actually
For matrix $R \in SO(3)$, we have properties like (eqn.2 is still unproved until now)
So, we gain
</center></p>
Take angular velocity’s form $\vec{\Omega}=I^{-1}\vec{L}$ into consideration,
This equation is the main equation that based on a rigid body system without outer force. Only variable $\vec{L}$ is unknown, so this first order differential equation can be solved with some initial condition.

Until now… I think it cannot fit the gimbal condition. Because gimbal is not free, it is always controlled by a hook. Anyway, we revise rigid body physics again.
See you!

Vector, matrix, tensor…
In cartesian coordinates, angular momentum has three directions: x, y, z.
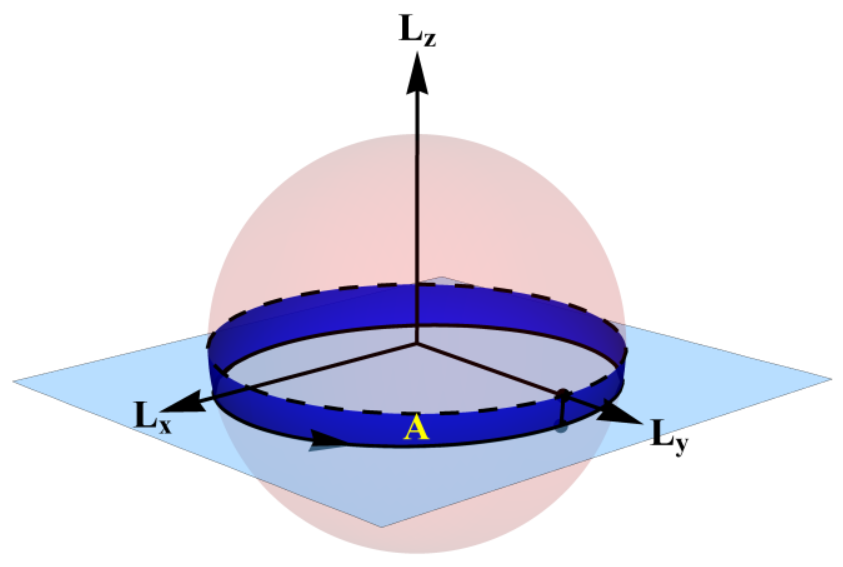
Ref: Dullin H R, Tong W. Twisting Somersault[J]. Physics, 2016.
So angular momentum L is a vector and each element describes one direction. Generally, we use Euler angles to analyze a rigid body system: $\alpha, \beta, \gamma$.
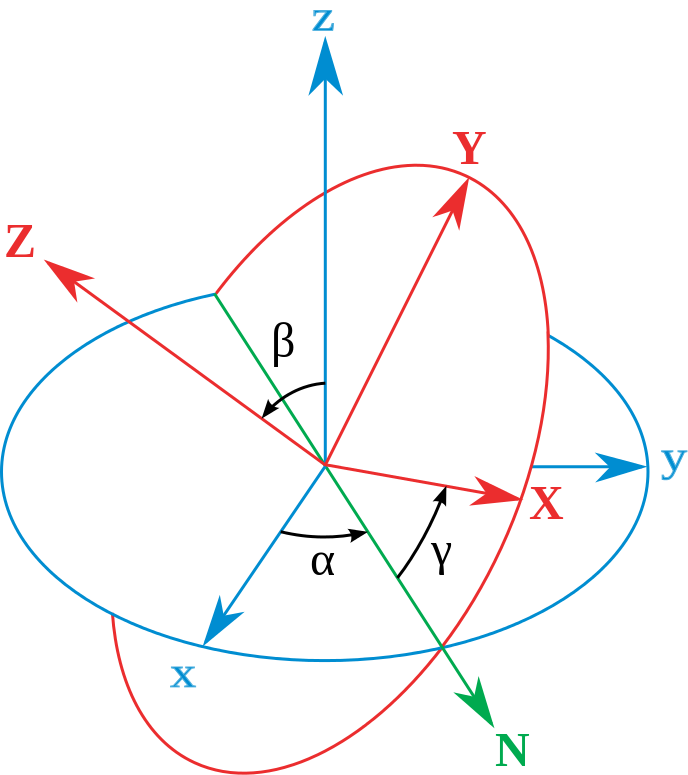
Ref: https://en.wikipedia.org/wiki/Euler_angles
Thus, angular velocity can be separated into three parts, which represent three rotation direction ($\alpha, \beta, \gamma$). Rotational inertia $I$ and rotational matrix $R$ are both $3 \times 3$ matrix. They can even be higher dimensional tensor. But I cannot understand it well now…
References
[1] Dullin H R, Tong W. Twisting Somersault[J]. Physics, 2016.
[2] Dullin H R. The Diver with a Rotor[J]. 2015.
[3] Tong W, Dullin H R. A New Twisting Somersault: 513XD[J]. Journal of Nonlinear Science, 2017, 27(6):2037-2061.