极限扩散电流到底是不是材料的本征性能？ | 基于K-L方程的RDE表面液流理论
写在前面
目前的主流研究认为，碱性环境中的氧还原反应（ORR）主要有两种反应途径。一种是四电子过程：
\[\text{O}_2 + 2\text{H}_2 \text{O} + 4\text{e}^- = 4\text{OH}^-\]一种是二电子过程：
\[\text{O}_2 + 2\text{H}_2 \text{O} + 2\text{e}^- = 2\text{H}_2 \text{O}_2\]四电子过程可以保证在更短的时间内提供更大的电流，即四电子过程可以保证更大的电池（fuel cell/metal-air batteries）功率。氧还原反应的电化学性能测试常使用基于K-L方程的旋转圆盘电极（RDE）方法对反应转移电子数进行测算。
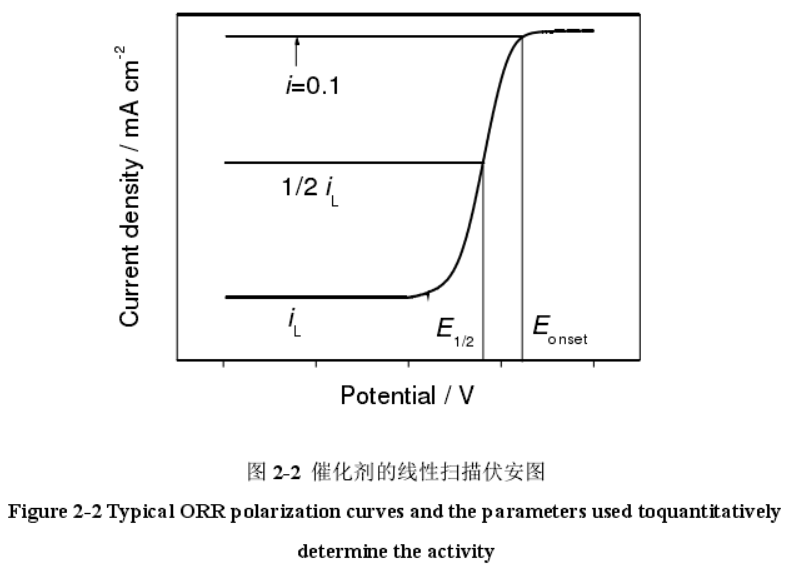
Ref: 周学俊. M-Nx/C类非贵金属氧还原催化材料的构筑及其电化学性能研究[D]. 东华大学, 2016.
K-L方程实际上建立了极限扩散电流$i_l$与旋转圆盘转速等物理因素之间的关系。通过不同转速下测试极限扩散电流，便可以拟合出关键的反应动力学参数——转移电子数。那么极限扩散电流到底是不是材料的本征性质呢？这个问题没有想象的那么简单，笔者首先介绍了K-L理论后我们再作判断不迟。
RDE下液流层的流体力学描述
如下图，建立RDE的柱坐标系。z = 0处为圆盘电极表面。
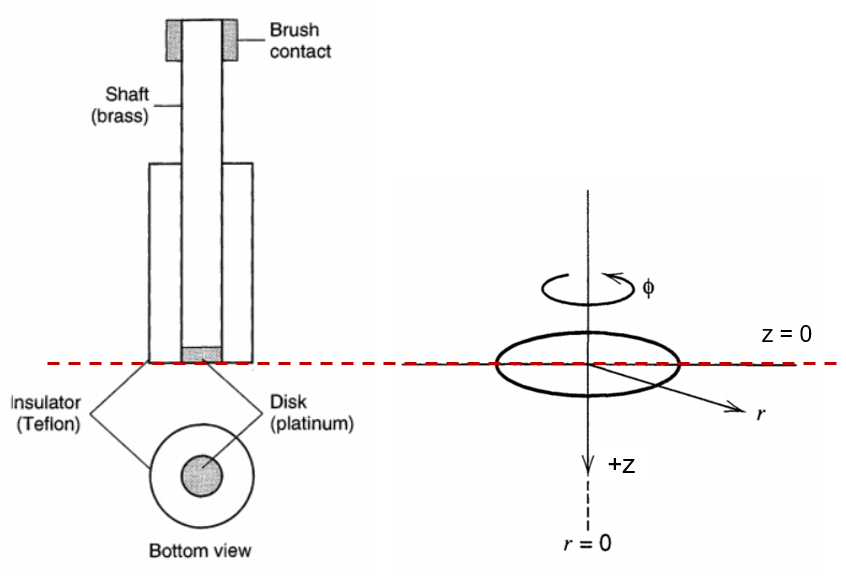
Ref: Bard et al., Electrochemical Methods: Fundamentals and Applications; wiley New York, 1980; Vol. 2.
定义液流速度
\[\vec{v} = (v_r, v_\phi, v_z)\]已知：
- 圆盘表面液体流速满足$v_r=0, v_phi=0, v_y=\omega r$.
- 本体溶液液体流速满足$v_r=0, v_phi=0, v_y=-U_0$.
由稳态下的纳维-斯托克斯方程（Navier–Stokes equations）可描述柱坐标下不同方向液体流速之间的关系
\[v_r + r \frac{\partial v_r}{\partial r} + r\frac{\partial v_z}{\partial z} = 0 \\ v_r \frac{\partial v_r}{\partial r} - \frac{v_\phi^2}{r} + v_z \frac{\partial v_r}{\partial z} = -\frac{1}{\rho} \frac{\partial p}{\partial r} + v_\phi \left[ \frac{\partial^2 v_r}{\partial r^2} + \frac{\partial}{\partial r}(\frac{v_r}{r}) + \frac{\partial^2 v_r}{\partial z^2} \right] \\ v_r \frac{\partial v_\phi}{\partial r} - \frac{v_r v_\phi}{r} + v_z \frac{\partial v_\phi}{\partial z} = v_\phi \left[ \frac{\partial^2 v_\phi}{\partial r^2} + \frac{\partial}{\partial r}(\frac{v_\phi}{r}) + \frac{\partial^2 v_\phi}{\partial z^2} \right] \\ v_r \frac{\partial v_z}{\partial r} + v_z \frac{\partial v_z}{\partial z} = -\frac{1}{\rho} \frac{\partial p}{\partial z} + v_\phi \left[ \frac{\partial^2 v_z}{\partial r^2} + \frac{1}{r} \frac{\partial v_z}{\partial r} + \frac{\partial^2 v_z}{\partial z^2} \right] \\\]Ref: Real-Ramirez, C. A., & Gonzalez-Trejo, J. I. (2011). Hydrodynamic Analysis of Electrochemical Cells. In Computational Simulations and Applications. IntechOpen.
von Karman在1921年提出以独立无量纲变量来描述各方向速度值，可以满足N-S方程的限制条件，即
\[\gamma = (\frac{\omega}{\mu})^{1/2} z\]其中$\omega$为圆盘转速，$\mu$为液体粘度. 此时定义
\[F(\gamma) = \frac{v_r}{r \omega}, G(\gamma) = \frac{v_\phi}{r \omega}, H(\gamma) = \frac{v_z}{\sqrt{\omega \mu}} \quad and \quad P(\gamma) = \frac{p}{\rho \mu \omega}\]可将N-S方程简化为
\[2F + H' = 0 \\ F'' - HF' - F^2 + G^2 = 0 \\ G'' - HG' - 2FG = 0 \\ H'' - HH' - P' = 0\]其边界条件为
\[H = F = P = 0, G = 1 \quad at \quad z = 0 \\ and \quad F = G = 0 \quad at \quad z = \infty \\\]Ref: von Kármán, T. (1921). Über laminare und turbulente reibung. Zeitschrift für Angewandte Mathematik und Mechanik, 1, 486.
Chochran在1934年提出使用无穷级数方法近似表示$F, G, H$三个函数。在离电极表面较近处，即$z$较小时，$\gamma << 1$，此时各方向速度值可表示为
\[v_r = r \omega F(\gamma) = r \omega (a \gamma - \frac{\gamma^2}{2} - \frac{b \gamma^3}{3} + \cdots) \\ v_\phi = r \omega G(\gamma) = r \omega (1 + b \gamma + \frac{a \gamma^2}{3} + \cdots) \\ v_z =(\omega \mu)^{1/2} H(\gamma) = (\omega \mu)^{1/2} (-\alpha \gamma + \frac{\gamma^3}{3} + \frac{b \gamma^4}{6} + \cdots)\]其中，$a=0.51026$，$b=-0.6159$。
Ref: Cochran, W. G. (1934). The flow due to a rotating disc. Proceedings of the Cambridge Philosophical Society, 30, 365-375.
在圆盘表面$z \rightarrow 0$，即$\gamma \rightarrow 0$，可以获得速度值表达式
\[v_r = r \omega (a \gamma) = -0.51 \omega^{2/3} \mu^{-1/2} r z \\ v_z = (\omega \mu)^{1/2} (-\alpha \gamma) = -0.51 \omega^{2/3} \mu^{-1/2} z^2\]RDE法向的物质对流及扩散
柱坐标下的反应物的对流-扩散方程可以写为
\[v_r (\frac{\partial C_o}{\partial r}) + \frac{v_\phi}{r} (\frac{\partial C_o}{\partial \phi}) + v_z (\frac{\partial C_o}{\partial z}) = D_o [\frac{\partial^2 C_o}{\partial z^2} + \frac{\partial^2 C_o}{\partial r^2} + \frac{1}{r} (\frac{\partial C_o}{\partial r}) + \frac{1}{r^2}\frac{\partial^2 C_o}{\partial \phi^2}]\]由于反应物浓度相对于RDE轴对称，即反应物浓度在$\phi$方向无差别，所以有
\[\frac{\partial C_o}{\partial \phi} = \frac{\partial^2 C_o}{\partial \phi^2} = 0\]在RDE表面径向上，在$0 \leq r \leq r_{disk}$，反应物浓度无差别，有
\[\frac{\partial C_o}{\partial r} = \frac{\partial^2 C_o}{\partial r^2} = 0\]因此可将反应物物质对流-扩散方程简化为
\[v_z (\frac{\partial C_o}{\partial z}) = D_o \frac{\partial^2 C_o}{\partial z^2}\]
将$v_z= -0.51 \omega^{2/3} v^{-1/2} z^2$代入上式得
\[\frac{\partial^2 C_o}{\partial z^2} = - \frac{z^2}{B} \frac{\partial C_o}{\partial z}\]其中，$B = \frac{D_o \omega^{-3/2} v^{-1/2}}{0.51}$. 接下来的任务就是对该偏微分方程进行积分处理，尝试求解。可以先令$X = \frac{\partial C_o}{\partial z}$，有
\[\frac{\partial X}{\partial z} = - \frac{z^2}{B} X\]两边积分可解得
\[\frac{X}{X_0} = \exp(-\frac{z^3}{3B})\]再将$X = \frac{\partial C_o}{\partial z}$带回，有
\[\frac{\partial C_o}{\partial z} = (\frac{\partial C_o}{\partial z})_{z=0} \exp(-\frac{z^3}{3B})\]这时候即将对该式进行二次积分。但是该次积分积分限的选取具有不同的物理意义。一种情形是电极表面的反应动力学很快，反应物一到电极表面就转化为产物，电极表面反应物浓度为零的情形。这种情况下，电流仅受到物质扩散传质的限制，我们称之为“极限电流情形”。另一种情形是电极表面的反应动力学没有那么快，电极表面反应物浓度不为零的情形，我们称之为“非极限电流情形”。接下来我们就来讨论分别描述这两种情形的Levich方程和Koutecky-Levich方程。
极限电流情形
在极限电流情形下，电极表面反应物浓度为零，则
\[\int_0^{C_o^*} dC_o = (\frac{\partial C_o}{\partial z})_{z=0} \int_0^\infty \exp(-\frac{z^3}{3B}) dz\]有定积分
\[\exp(a z^3) dz = (-a)^{1/3} \Gamma(\frac{4}{3}) = 0.8934(-a)^{1/3}\]其中$\Gamma$函数为
\[\Gamma(x) = \int_0^\infty t^{x-1} e^{-t} dt\]其在[0,3]区间的函数图像如下
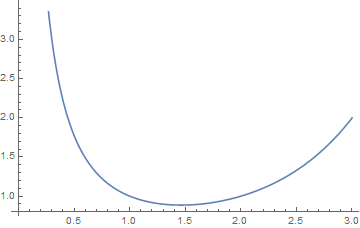
故
\[C_o^* = (\frac{\partial C_o}{\partial z})_{z=0} 0.8934(3B)^{1/3} = (\frac{\partial C_o}{\partial z})_{z=0} 0.8934(\frac{3D_o \omega^{-3/2} \mu^{1/2}}{0.51})^{1/3}\]又因为电流与电极表面的物质流量相关，由法拉第定律可得
\[i = nFAD_o (\frac{\partial C_o}{\partial z})_{z=0}\]与上式联立可得Levich方程
\[i_l = 0.62 nFAD^{2/3} \omega^{1/2} \mu^{-1/6} C_o^*\]
从上式我们已经可以知道，对特定电极反应（转移电子数n不变），极限扩散电流是旋转圆盘转速的函数——因为法拉第常数$F$、电极面积$A$、圆盘尺寸、电解液中反应物扩散系数$D$、电解液粘度$\mu$和电解液浓度$C_o^*$都是恒定的。对不同材料，氧还原所经历路径不同，也就可能导致电极表面的电极反应不同，会反应在转移电子数上，从而导致极限扩散电流的不同。因此，本文的结论就是，在正确的表征方法下，极限扩散电流是材料的本征性质（活性位点催化选择反应路径的性质）。
非极限电流情形
在非极限电流情形下，电极表面反应物浓度不为零，则
\[\int_{C_o(z=0)}^{C_o^*} dC_o = C_o^* - C_o(z=0) = (\frac{\partial C_o}{\partial z})_{z=0} \int_0^\infty \exp(-\frac{z^3}{3B}) dz\]且$C_o(z=0) \neq 0$. 同极限电流情形进行积分可得
\[i_l = 0.62 nFAD^{2/3} \omega^{1/2} \mu^{-1/6} [C_o^* - C_o(z=0)]\]由Levich方程可得
\[i = i_l [\frac{C_o^* - C_o(z=0)}{C_o^*}]\]对单步骤完全不可逆反应过程有
\[i = nFAk_f(E)C_o(z=0)\]其中反应速率常数$k_f(E) = k_0 \exp[-\alpha f(E-E^\Theta)]$可由反应动力学B-V方程导出。那么该式与上式联立可得
\[i = nFAk_f(E) C_o^*(1-\frac{i}{i_l})\]可以定义
\[i_k = nFAk_f(E)C_o^*\]那么便有Koutecky-Levich方程
\[\frac{1}{i} = \frac{1}{i_k} + \frac{1}{i_l} = \frac{1}{i_k} + \frac{1}{0.62 nFAD^{2/3} \omega^{1/2} \mu^{-1/6} C_o^*}\]
从上式我们可以看出，Levich方程所描述的极限电流情形是Koutecky-Levich方程中$i_k \rightarrow \infty$时的情形。K-L方程的物理意义是：在无表面修饰的电极上，总电流主要由反应动力学导致的电流$i_k$和传质所导致的电流$i_l$构成。
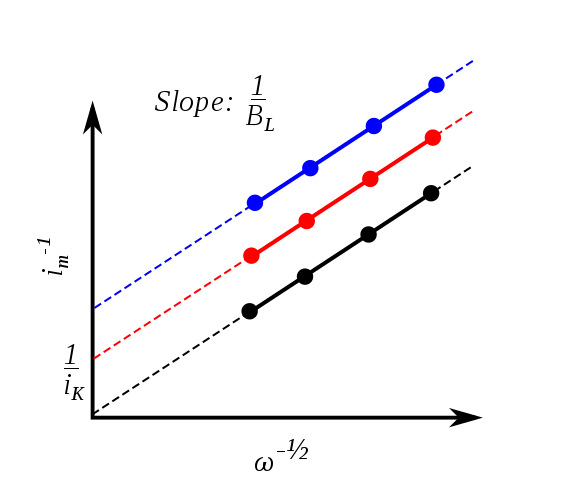
如果电极的表面物理化学性质发生变化（也即电极经过表面修饰），那么反应的转移电子数必定会发生变化，从而反映在K-L拟合直线的斜率上。当然，这个变化也会反映在拟合直线的截距$\frac{1}{i_k}$上，但其中含有$k_f(E)$这一不易确定的反应动力学参数，所以其不容易被定量分析。
理论上可以通过取不同电压的电流和转速作图，便能够获得不同电压的转移电子数。要更明确地得到不同电位下的转移电子数，需要采用旋转环盘电极（RRDE）方法。旋转环盘电极方法在笔者之前的博文中有介绍其原理（氧还原反应（Oxygen Reduction Reaction）基础）。
写在后面
总结本文得到的结论：
- 如果电极的表面物理化学性质发生变化（也即电极经过表面修饰），那么反应的转移电子数必定会发生变化，从而反映在K-L方程拟合直线的斜率和截距上。
- 在正确的表征方法下，极限扩散电流是材料的本征性质（活性位点催化选择反应路径的性质）。
- 负载量可能会通过活性位点暴露的角度对极限扩散电流产生影响。但在一定范围内，其影响可能是不大的。
在ORR测试中，需要通过K-L方程计算不同偏压下的转移电子数。这时候一定要注意各数值的量纲问题！在转速使用“rpm”（Revolutions Per Minute，圈/分）时，常数取“0.2”，[5] 即使用公式：$i_l = 0.2 nFAD_o^{2/3} \omega^{1/2} \mu^{-1/6} C_o^*$；在转速使用“rad/s”（Radian Per Second，弧度/秒）时，常数取“0.62”，[6] 即使用公式：$i_l = 0.62 nFAD_o^{2/3} \omega^{1/2} \mu^{-1/6} C_o^*$（如果纵坐标已经取电流密度，记得将等式右边的A略掉）。
ORR计算常用物理常数：法拉第常数$F=96485 C mol^{-1}$，氧气在电解液中的饱和浓度$C_o = 1.2 \times 10^{-3} mol L^{-1}$，氧气在KOH溶液中的扩散系数$D_o = 1.9 \times 10^{-5} cm s^{-1}$，电解液粘度$\mu = 0.01 cm^2 s^{-1}$.
总之，极限扩散电流影响因素较多，非预期的实验结果一定要仔细分析！
参考文献
[1] Bard, A. J., Faulkner, L. R., Leddy, J., & Zoski, C. G. (1980). Electrochemical methods: fundamentals and applications (Vol. 2). New York: wiley.
[2] Real-Ramirez, C. A., & Gonzalez-Trejo, J. I. (2011). Hydrodynamic Analysis of Electrochemical Cells. In Computational Simulations and Applications. IntechOpen.
[3] von Kármán, T. (1921). Über laminare und turbulente reibung. Zeitschrift für Angewandte Mathematik und Mechanik, 1, 486.
[4] Cochran, W. G. (1934). The flow due to a rotating disc. Proceedings of the Cambridge Philosophical Society, 30, 365-375.
[5] Han S, Hu X, Wang J, et al. Novel Route to Fe‐Based Cathode as an Efficient Bifunctional Catalysts for Rechargeable Zn–Air Battery[J]. Advanced Energy Materials, 2018, 8(22): 1800955.
[6] Liang Y, Li Y, Wang H, et al. Co 3 O 4 nanocrystals on graphene as a synergistic catalyst for oxygen reduction reaction[J]. Nature materials, 2011, 10(10): 780-786.